Perfect Reconstruction: Short-Time Fourier Transform (STFT) dan Invers-nya menggunakan half-cycle sine window

Short-time Fourier Transform (STFT) artinya transformasi fourier dari masing-masing blok sinyal yang diperoleh dari proses windowing suatu sinyal. Seperti yang sudah kita ketahui sebelumnya, jika kita menerapkan fft pada suatu sinyal, kita hanya akan mendapatkan informasi frekuensi dengan cukup akurat namun tanpa informasi waktu dari suatu sinyal dan begitu pula sebaliknya. Nah STFT menjembatani dua hal tersebut, pada saat yang bersamaan STFT akan memberikan informasi waktu dan frekuensi secara temporal. Untuk lebih jelasnya mari kita coba membuat STFT menggunakan Octave. 


Pastikan komputer anda sudah terinstall octave disini.

Short-Time Fourier Transform (STFT)

Window yang digunakan adalah setengah sinus seperti pada persamaan di bawah ini.

$\omega (n) = \sin \Big(\frac{\pi}{N}(n+0.5)\Big), \ \ \ n = 0, ..., N - 1$

dimana $N$ adalah panjang window. Overlapping antar window adalah 50% dari panjang window. Nilai ini dipilih untuk mendapatkan "perfect reconstruction" saat melakukan invers. STFT diperoleh dengan cara mentransformasikan sinyal untuk masing-masing window ke domain frekuensi seperti pada persamaan di bawah ini.

$S(m,\omega) = \textrm{DTFT}\{x(n) \cdot \omega(n-m \cdot N/2)\}$

dimana $\omega$ adalah indek frekuensi dan $m$ adalah indek waktu. Simpan code berikut ini dengan nama "stft_sin.m"

==============================================

function X = stft_sin(x,N,nfft)

% vektor baris
n = [0:N-1]';
x = x';

% Zero-padding
ncol = ceil(2*(length(x)-N/2)/N);
if (ncol+1)*N/2 > length(x)
  x = [x; zeros((ncol+1)*N/2-length(x),1)];
end
x = [zeros(N/2,1); x; zeros(N/2,1)];

% Window sinus
Nindex = (length(x)-N/2)*2/N;
window = repmat(sin((n+0.5)*pi/(N)),1,Nindex);

% Proses Windowing
colindex = 1+ (0:Nindex-1)*(N/2);
rowindex = n+1;
y = zeros(N,Nindex);
y(:) = x(rowindex(:,ones(1,Nindex))+ colindex(ones(N,1),:)-1);
y = y.*window;

% FFT
X = fft(y,nfft);
X = X(1:nfft/2+1,:);

==============================================

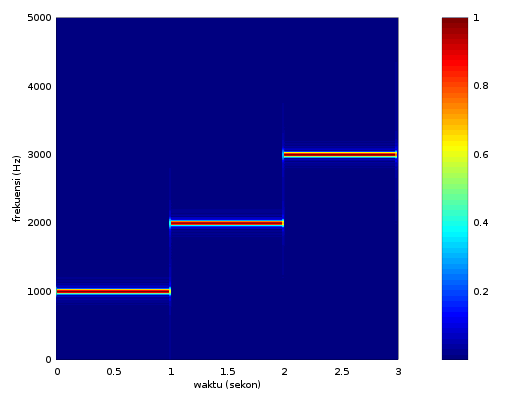
Untuk menguji "stft_sin.m" berjalan dengan baik atau tidak, kita akan membangkitkan sinyal seperti pada persamaan berikut ini

$x(n) \begin{cases} \sin(2 \pi 1000 n) & \quad \text{if } \ \  t \geq 0 \ \ \& \ \ t < 1 \\ \sin(2 \pi 2000 n) & \quad \text{if } \ \ t \geq 1 \ \ \& \ \ t < 2 \\  \sin(2 \pi 3000 n) & \quad \text{if } \ \  t \geq 2 \ \ \& \ \ t < 3 \\   \end{cases}$

dan mentransformasikannya ke domain waktu-frekuensi untuk mengetahui apakah program kita sudah benar atau belum. Untuk mengeceknya cukup program di bawah ini

==============================================
close all
clear
clc

% Sinyal
fs = 10000;
t = 0:1/fs:3;
x = zeros(size(t));
for i = 1:3
  range_t = double(t>=(i-1)*max(t)/3 & t <i*max(t)/3);
  x = x + sin(2*pi*1000*i*t).*range_t; 
end

% STFT
nfft = 1024;
N = nfft/4;
X = stft_sin(x,N,nfft);

% plot
F = linspace(0,1,size(X,2))*fs/2;
T = linspace(min(t),max(t),size(X,1));
figure
imagesc(T,F,abs(X)/max(max(abs(X))))
colorbar()
axis xy
axis square
xlabel('waktu (sekon)')
ylabel('frekuensi (Hz)')
============================================== 

Invers Short-Time Fourier Transform (ISTFT)

 Berikut ini merupakan persamaan untuk ISTFT

$x(n) = \frac{\displaystyle \sum_{m} s(m,n) \cdot \omega(n-m \cdot N/2)}{\displaystyle \sum_{m} p(n-m \cdot N/2)}$

 

 dimana

$s(m,n) = \textrm{DTFT}^{-1} \{S(m,\omega)\}$

$p(n) = \omega^2(n)$

dan Invers ini dikatakan "perfect reconstruction" jika memenuhi kondisi sebagai berikut.

$\displaystyle \sum_{m} p(n-m \cdot N/2) = 1$

Selanjutnya, Simpan code berikut ini dengan nama "istft_sin.m".

==============================================
function x = istft_sin(X,N,ndata)

% IFFT
X = [X; conj(X(end-1:-1:2,:))];
s = real(ifft(X));
s = s(1:N,:);
x = zeros(1,(size(s,2)+1)*N/2);
x = x(:);
p = x;

% Window sinus
n = 0:N-1; n=n(:);
window = repmat(sin((n+0.5)*pi/(N)),1,size(X,2));

for i = 1:size(X,2)
  x(1+(i-1)*N/2:(i+1)*N/2) = x(1+(i-1)*N/2:(i+1)*N/2) + s(:,i).*window(:,i);
  p(1+(i-1)*N/2:(i+1)*N/2) = p(1+(i-1)*N/2:(i+1)*N/2) + window(:,i).^2;
end
x = x./p;
x = x(N/2+1:ndata+N/2);
x = x';
==============================================

dan run program berikut ini untuk mengecek apakah sinyal sebelum dan sesudah invers adalah sama (perfect reconstruction).

==============================================
close all
clear
clc


fs = 10000;
t = 0:1/fs:3;
x = zeros(size(t));
for i = 1:3
  range_t = double(t>=(i-1)*max(t)/3 & t <i*max(t)/3);
  x = x + sin(2*pi*5*i*t).*range_t; 
end

% STFT
nfft = 1024;
N = nfft/4;
X = stft_sin(x,N,nfft);

% ISTFT
ndata = length(t);
xnew = istft_sin(X,N,ndata);

figure
subplot(211)
plot(t,x,'LineWidth',1)
ylim([-1.1 1.1])
subplot(212)
plot(t,xnew,'LineWidth',1)
ylim([-1.1 1.1])

% Cek nilai perbedaan maksimum
max(abs(x-xnew))
==============================================

 

 Code-nya dapat didownload di link ini.

 Selamat mencoba dan semoga bermanfaat.

Referensi

Ivan W. Selesnick, Short-Time Fourier Transform and Its Inverse, April 14, 2009